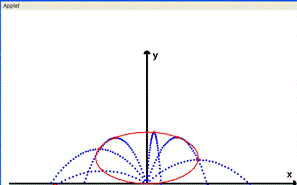
Questa applet riguarda il moto del proiettile rivisitato allo scopo di mettere in evidenza delle proprietà connesse con lo studio delle sezioni coniche.
Questa applet ha lo scopo di mostrare le proprietà matematiche (per la dimostrazione vedi Approfondimenti) di detto moto, fornendo così al docente l'opportunità di intraprendere un percorso didattico utile per introdurre il concetto di sezioni coniche in un modo diverso dal solito, ma più accattivante per gli studenti.
Infatti, fissato il modulo della velocità iniziale, si può interattivamente mostrare che:
• l'inviluppo delle diverse parabole, ottenibili per diversi angoli di tiro, è ancora una parabola;
• il luogo geometrico dei vertici è una ellisse;
• il luogo geometrico dei vari fuochi è una circonferenza.
L'applet sul moto del proiettile presenta, a destra (Fig.1), un pannello di controllo contenente due cursori per selezionare la velocità iniziale e l'angolo di tiro del proiettile e tre pulsanti che permettono, rispettivamente, di avviare, accelerare l'animazione e di pulire lo schermo.
Infine sono presenti i tre pulsanti di scelta necessari per visualizzare le coniche :
Fig.1.
La figura mostra in colore blu le traiettorie del proiettile, a fissata velocità iniziale e a differenti angoli di tiro, mentre in rosso è mostrato il luogo geometrico dei massimi delle traiettorie. A destra dell'applet è presente il pannello di controllo per controllare l''animazione.
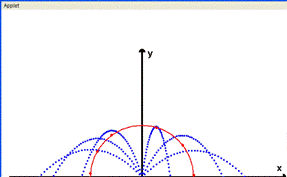
Fig.2.
La figura mostra in blu le traiettorie del proiettile ed in rosso la circonferenza, luogo geometrico dei fuochi delle traiettorie.
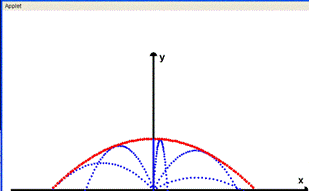
Fig.3.
In questa figura è mostrata, in colore rosso, la parabola che costituisce l'inviluppo delle traiettorie del proiettile .
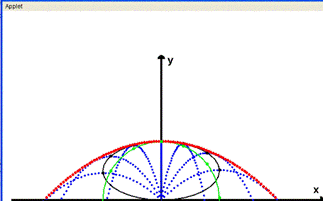
Fig.4.
Nella figura sono mostrate le traiettorie del proiettile in blu ed in colore rosso, nero e verde, rispettivamente, l'inviluppo, il luogo geometrico dei massimi e quello dei fuochi delle traiettorie .
Approfondimenti
1. Inviluppo delle traiettorie paraboliche
Per capire la relazione tra inviluppo e traiettorie di proiettili, con uguale velocità iniziale,
, ricordiamo che la generica traiettoria di un proiettile è espressa da:
Questa equazione può essere riscritta come:
dove abbiamo indicato
e
.
Imponendo che l'equazione (2) abbia 
otteniamo l'equazione dell'inviluppo:
detta “parabola di sicurezza”.
L'inviluppo delle traiettorie dei proiettili può rappresentare anche una traiettoria, ed in questo caso corrisponde alla traiettoria di un proiettile che ha il doppio della velocità iniziale dei proiettili considerati, angolo di tiro pari a 45°, posizione di lancio x = -R e massima altezza y = R/2 per x = 0 .
2. Luogo geometrico dei vertici delle traiettorie paraboliche
La seguente proprietà riguarda il legame tra una ellisse e le traiettorie dei proiettili. Questa ellisse appare come la curva che congiunge i punti di massima altezza delle traiettorie paraboliche tracciate dai proiettili lanciati, dall'origine di un sistema di riferimento, con uguale velocità iniziale
. E' noto che per i proiettili valgono le equazioni:
dove 
è l'angolo di tiro.
Il tempo impiegato per raggiungere la massima altezza è 
così le coordinate del proiettile al tempo
sono: 
e
dove
è la massima altezza raggiunta e
corrisponde alla coordinata orizzontale, cioè rappresentano il vertice delle parabole 
.
Con l'aiuto delle identità trigonometriche: 
e
, le coordinate
e
possono essere riscritte come segue:
e
Eliminando l'angolo 
si ottiene il luogo dei punti di massima altezza:
dove abbiamo definito
e
,
cioè a = 2b .
Il luogo dei punti ottenuto rappresenta una ellisse centrata nel punto (0,b) con asse minore e maggiore dato da 2b e 2a , rispettivamente.
3. Luogo geometrico dei fuochi delle traiettorie
Per quanto riguarda questa proprietà, noto che la traiettoria è espressa da :
poniamo
e
per cui
l'equazione (1) può essere riscritta:
.
Il fuoco di questa parabola è dato da:
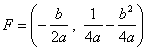
andando a sostituire i valori di a e b si arriva a :
.
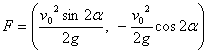Poniamo
e scriviamo le coordinate dei fuochi:
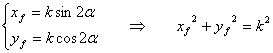
che è l'equazione di una circonferenza di centro (0,0) e raggio r = k .